The Drought…
Everyone in the Cape must be acutely aware of the drought by now. Yes… we’re in the middle of it… Perhaps the idea has not fully crystallized in the minds of a couple of thirsty dwellers of Claremont and Constantia, who still guzzle 2-3 thousand of liters of water per person per day (or so the press reports), while almost everyone else goes to extreme lengths to keep their water use near the magical number of eighty and seven. But I understand the guzzler’s water meters are being fitted with water management devices, which is a city-speak for an aptly named stopcock, and so the reality will hopefully dawn on the “waterheads” too.
In the meantime, for the last couple of weeks, we’ve all been watching rain fall and its annual total rise, hoping for some reprieve from running around bathrooms with buckets, and frantic purchases of ridiculously overpriced rainwater tanks. It hasn’t happened. Rainfall has been meagre. The rainy season is about to finish, and we have what we have – dams at 32%, compared to last year’s 58% . Even if there are good late rains, they are not going to change the predicament of every single one of us who cannot afford to drill a borehole in their backyard. Hopefully, the planned “revolutionary” transformation of the Cape Town’s water supply system will bear fruit, promises of the city will stand true, and there will be no “day zero”. But we will only know this next June/July.
But since the season is slowly ending, it’s time for a summary – and for an answer to the question posed in the title.
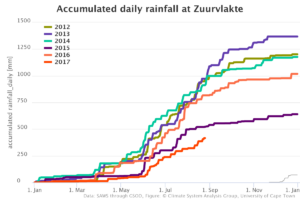
Perhaps you have seen “Cape Town rainfall monitor”, aka “The Graph”? If you haven’t, here it goes:
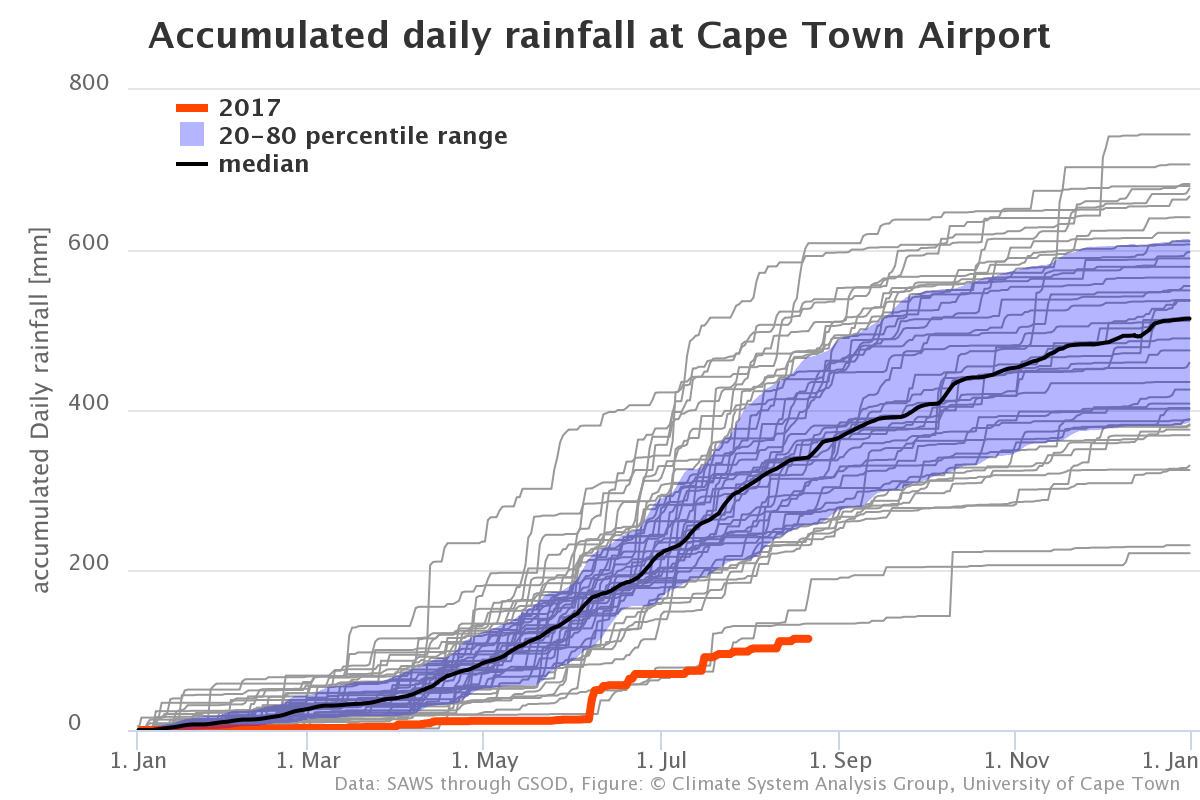
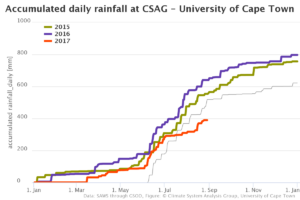
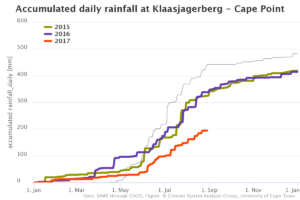
and here go several other ones that are available for locations in the Western Cape:
This is where we are now. The total rainfall at the Cape Town airport (CTA) is so far below that experienced in the same part of the year during the last 40 years. The other stations do not have that many years of data available, but they show a similar pattern – this year’s rainfall is substantially lower than the rainfall in the last 4-6 years.
But, of course, in any 41 years, there must be a year that has the lowest rainfall, so why not now? Indeed. Droughts happen. But even without much statistical or climatological knowledge, we would all have a tingling in the back of our heads that there might be strong droughts, and mild droughts, and perhaps even a sensation that strong droughts happen less frequently than mild ones.
Returning droughts
Some time ago, I’ve heard a story told by an old Kenyan herdsman. The Madala said that every now and then, his village experienced a cattle-killing drought. Every decade, or so, they experienced a goat-killing drought (goats being more sturdy than cows, would die only if conditions were more extreme). And once in a man’s (woman’s of course too) lifetime, they would experience a man-killing drought.
So is Cape’s drought cattle-, goat- or man-killing one? This question can, of course, be rephrased in scientific terms – what is the return interval of the drought we are experiencing? Which basically means: how often, on average, can we expect a drought of a magnitude of the one that we have now, or more severe, to occur?
Let’s have a look!
Drought is a relatively complex concept, particularly the hydrological drought. And it is the hydrological drought that affects Cape’s dams. A hydrological drought may be a result of a nuanced interplay of characteristics of the rainy season such as timing, magnitude and intensity of rainfall events. So in theory, to quantify the current drought, one would need to translate these rainfall characteristics into hydrological responses such as surface and groundwater runoff, combine them into inflow to the reservoirs or dams and take into account the actual evaporation as well as the dynamics of water abstractions. Yes, perhaps one day I’ll do all that. But this is not that day. Today, I will just use the bluntest approach available – I will look at the total annual rainfall to characterize the drought. Which is ok, because the current drought does not appear to be intricate. Rather, it is simply crude and rough.
The decision to focus on total annual rainfall makes things simple. To determine how often is the current drought expected to occur, I just need to fit a probability distribution function to observed total annual rainfall data and determine where on that function this year’s rainfall value falls. That value can then be translated into more informative indices such as probability of non-exceedance (i.e. probability that in any single year rainfall will not exceed this year’s value), or return interval (i.e. a number of years that, on average, separate years with rainfall similar to this year’s), or frequency of occurrence (i.e. how frequently do years similar to this year occur). For the uninitiated, this translates into “normal human” as follows: based on past observations, I need to determine how frequently years with annual total rainfall of various magnitudes happened in the past. There should be a relationship between how frequently a given annual rainfall occurred, and its magnitude. I can use that relationship to describe how frequently the rainfall observed in 2017 is expected to happen “in general”.
Let’s bring the data!
What? There aren’t much?
Yup. There aren’t much.
The figures above are basically all of relevance to the task that CSAG have at the moment. We do have access to other datasets, such as the country-wide rainfall records by SAWS or ARC, but these data do not come to us very fast. Currently, we only have SAWS data until the end of 2015, and we are negotiating the update. Data from other sources, such as those used to plot the figures above, are either very short (2-6 years), or are of bad quality. The Cape Town airport (CTA) is but the only station in Western Cape with good quality data available through GSOD – a global meteorological data repository used by weather forecasters and aeronautics sector. And satellite rainfall data, unfortunately, capture Western Cape rainfall in a rather unrealistic fashion.
I can, of course, perform the analysis using the available 41 years of GSOD data for CTA that are the basis for “Cape Town rainfall monitor”. But that wouldn’t be very robust – this is a relatively short time series, and the uncertainty of my estimates would be rather large.
I think that a better solution is to use the CTA data to estimate the last two years of rainfall at one of the SAWS station for which a longer time series is available.
The data
So after searching through the SAWS datasets, I have found Altydgedacht station, which is located in Bellville, not very far from the Cape Town airport, and has a very similar rainfall regime to that recorded at CTA, and only three years missing in the 1923-2015 record.
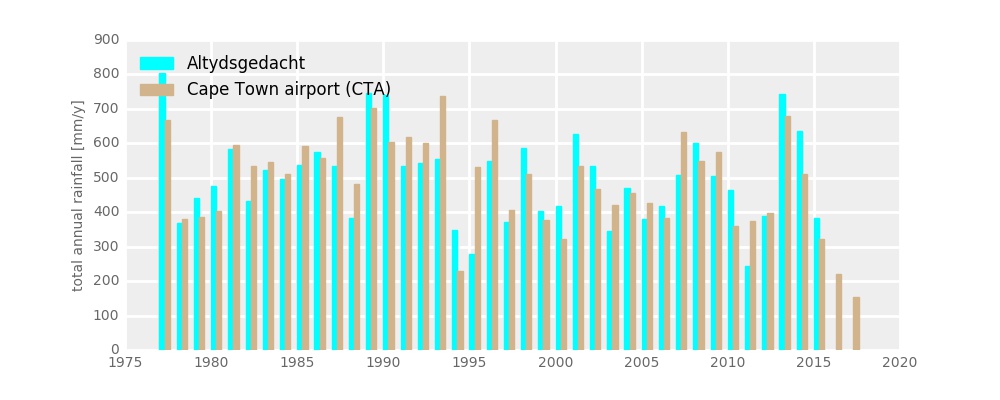
I have filled the three missing years (1929, 1946 and 1947) with the long-term mean annual rainfall, and estimated the 2016-2017 total in the following way:
– currently (on 25 August) CTA station’s accumulated rainfall (i.e. the total recorded between 1 Jan 2017 and 25 Aug 2017) stands at 114 mm, which is 31% of that station’s mean of 1977-2016 1 Jan-25 Aug rainfall, i.e. of 366mm.
– the 1977-2015 mean of the accumulated rainfall at the end of the year (i.e. on 31 Dec), or simply the mean annual rainfall, is 506mm. My crude guess of the 2017 total is thus 31% of that, i.e. 157mm.
– the 2016 rainfall total, recorded at CTA is 221mm, which is 43% of the 1977-2015 mean of 506mm.
– now, I consider that the 2017’s 31% and 2016’s 43% of mean annual rainfall at CTA are also true for the Altydgedacht station. From that, I can estimate the 2017 and 2016 totals at that station. Because the 1977-2015 mean at Altydgedacht is 502mm, my estimate for 2016 total is 218mm and for 2017 is 153mm.
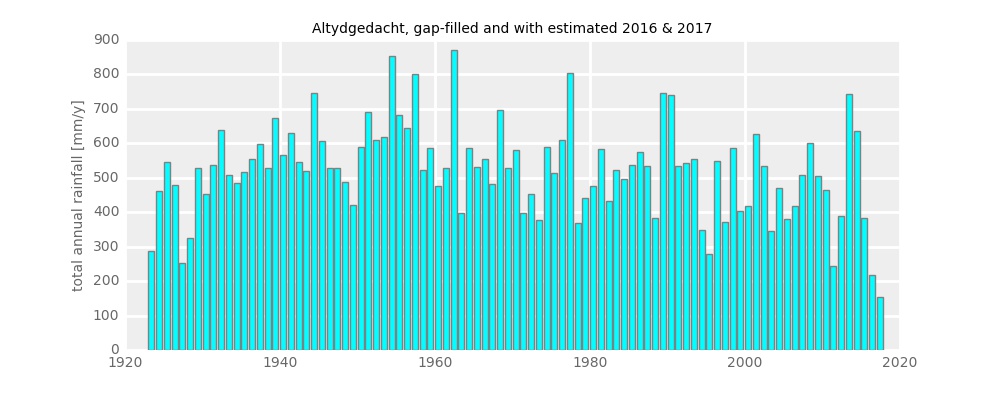
With that, the Altydgedacht’s time series looks like this:
Frequency distribution
Now I need to determine a function that describes frequency distribution of total annual rainfall at Altydgedacht. One can expect that distribution to be either normal, or of gamma family. The histogram of data with fitted normal density function looks like this:
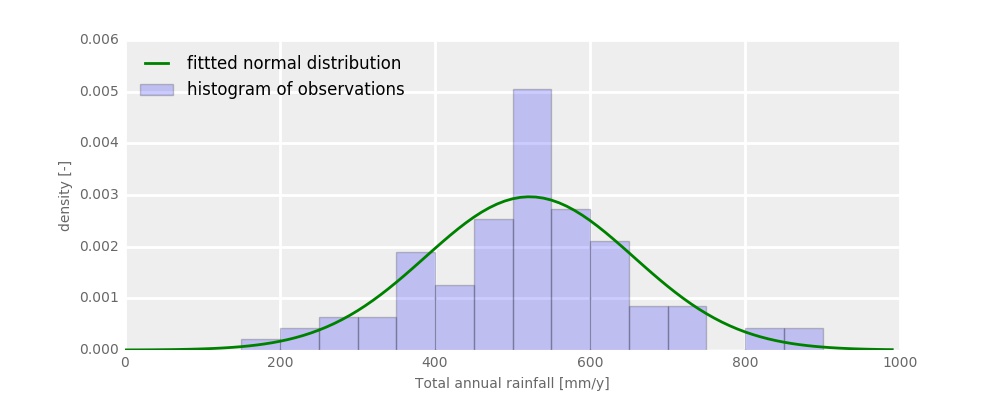
Clearly, the normal distribution describes observations relatively well. I have in fact tested that the data is approximately normally distributed with an appropriate test: Wilk-Shapiro, a test for normality, does not reject my assumption that that data follows the normal distribution (its p-value is 0.32). Just to test things, I have also fitted the gamma distribution, but the fit turned out to be almost exactly the same as that of the normal distribution, so I decided to stick to the simpler solution, i.e. the normal distribution.
Return interval
Now, based on that fitted normal distribution, the Altydgedacht’s 2017 estimated rainfall (153mm/year) corresponds to the 0.00306 quantile, and thus is expected to occur 1/0.00306 or once in 325 years. In other words, the return interval of the 2017 rainfall level is 325 years.
I can also calculate the uncertainty of that estimate. For that, I apply my favourite statistical method, i.e. the bootstrap. Bootstrapping is simply drawing a large number of random samples from the analysed data, and calculating the thing one wants to calculate from those samples, rather than from the original data. That gives a range (actually a distribution) of possible outcomes on the desired calculation/index that is conditioned on the source data, and takes into account the fact that the data themselves are actually a random sample of some larger, underlying “population”. The bootstrap is a standard way of calculating uncertainty of more complex statistical indices.
The bootstrap distribution of 100000 “samples” of the return interval for 2017’s rainfall at Altydgedacht looks like this:
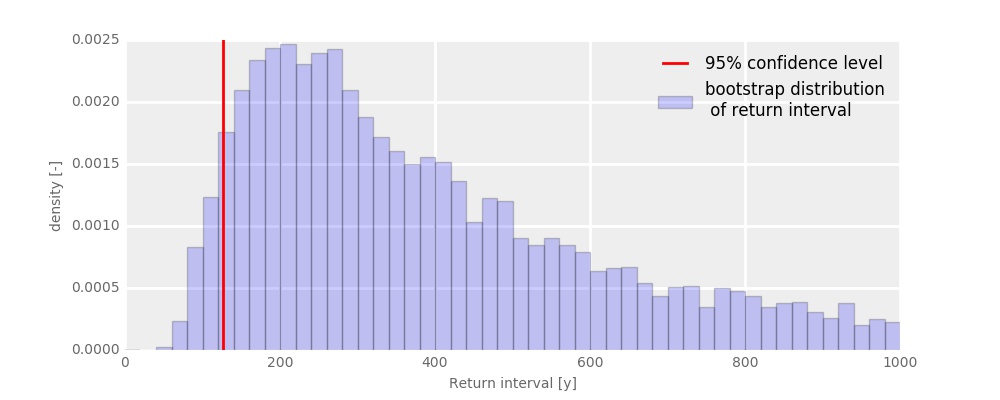
As this figure illustrates, the uncertainty of the above estimate of return interval (of 325 years) is rather large. But, based on the distribution shown in this figure, we can determine that there is a 95% probability that the “true” value of the return interval of 2017 rainfall is more than 126 years.
Pretty rare. Pretty strong. Pretty scary. But that’s not the end of the story.
Firstly… the trend
There is a long-term trend in rainfall at Altydgedacht, and that trend might partly be responsible for the low rainfall of 2017. We can assess the effect of that trend on the return interval of the current drought by simply repeating the above analysis on detrended data. The detrending process is simply removing the long term trend as so:
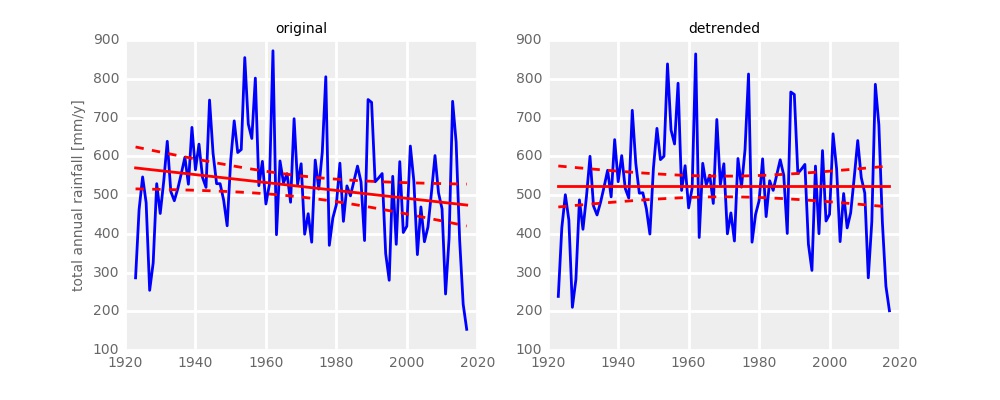
For the detrended data, the estimate of the return interval of 2017 rainfall is 135 years, and there is a 95% probability that its “true” value is more than 63 years. It thus appears that the trend in data has about doubled the frequency of low rainfall years. What drives the trend? I’m not sure. It can be anthropogenic climate change, but we cannot confirm that at this stage. Long-term trends in rainfall in Western Cape vary depending on location, so one cannot be sure without a more in-depth analysis.
Secondly… multiple years
We can and actually should take a look at a multi-year drought. This is because it’s not only 2017 that matters. Should the low rainfall of 2017 follow up on a wet year, the water situation in the Cape wouldn’t be that dire. It has, however, followed a relatively dry year, we have started the 2017 season with already low dam storages, and we are where we are now. Figures below illustrate time series of 2 to 5-year mean rainfall at Altydgedacht:
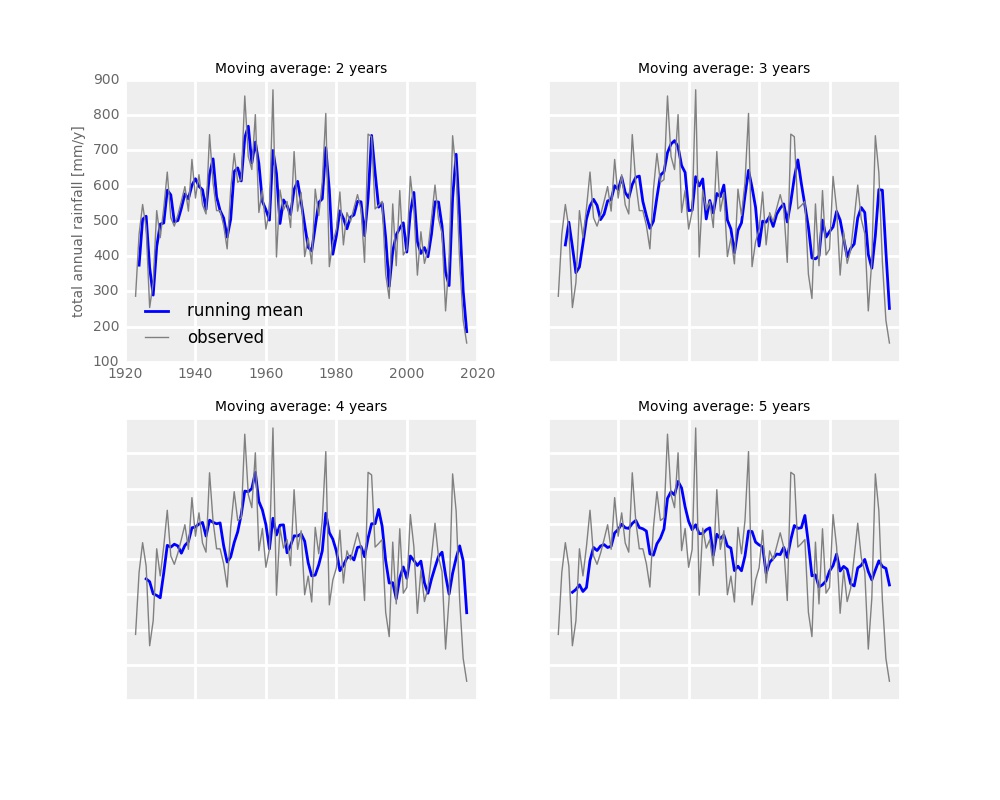
For 2 to 4 years rainfall means, the recent period is indeed the driest since the mid-1920s. The driest 5 years, were, however, recorded past then. This means that the total rainfall delivered over the last 5 years was not particularly exceptional. But the 2, 3 an 4-year was.
I can potentially repeat the frequency of occurrence calculations based on 2, 3 and 4-year totals. However, calculating the frequency of occurrence of multi-year droughts requires some special effort, because of autocorrelation. Simply, the year-on-year sequencing of rainfall is not totally random. The wet years are likely to follow wet years. Dry years are likely to follow dry years. That’s autocorrelation. That autocorrelation makes the sequences of dry years more likely, compared to that if there was no year-on-year correlation. We have to account for that in our calculations if the autocorrelation is strong.
The lag-1 autocorrelation (i.e. correlation between rainfall total of two consecutive years) in the Altydgedacht data is 0.25, which is actually relatively high for year-on-year autocorrelation, and that value is significant at 0.02 level (which means we can be rather confident it is real, and not spurious or accidental). It seems, thus, that I have to take that autocorrelation into account in the multi-year analyses.
To calculate the return interval of 2-5 year means, accounting for autocorrelation, I have done as follows:
– generated a synthetic long time series (say 100000 years) of data that had an identical mean, variance and lag-1 autocorrelation to that of the Altydgedacht time series,
– calculated a 2-year moving average of that series,
– counted how many times a value lower or equal to the mean 2-year (i.e. 2016-2017) Altydgedacht rainfall occurred in that synthetic time series.
– repeated the above for 3, 4 and 5-year moving averages.
These are the resulting return intervals:
2-year (2016-2017) rainfall: 1150 years
3-year (2015-2017) rainfall: 628 years
4-year (2014-2017) rainfall: 63 years
5-year (2013-2017) rainfall: 10 years
The 2 and 3-year events are very, very rare. Calculations on the detrended time series reveal, similarly to those performed on one-year data, that the trend has decreased the return interval, i.e. increased the frequency or in other words the risk of observed events. However, unlike for individual year, that risk has increased by a factor of 3 to 4.
So what?
Well, two things. Firstly – the above results should make one think hard about anthropogenic climate change as a possible driver of the trend.
Secondly – I have an impression that the results somewhat exonerate the Cape’s government, as well as water engineers designing the Cape Town’s water supply system from blame for the current water crisis. Water supply systems are usually designed with an assurance rate of 97%, which means that in worst case they may fail only 3% of time. The conditions we experience now seem to be well beyond what one usually plans for. If my calculations are right, for the water supply system to go through this drought unscathed, its assurance level should be 99.9%. Surely one can implement a system like that, but firstly, who is going to foot the bill, and secondly, even this might be difficult if the climate goalposts are being shifted.
Footnote
And now a footnote. One has to realize that all the above calculations hang very strongly on observed data from a single station, i.e. Cape Town airport. It is possible that the rainfall there is underreported and thus the analysed events are not as rare as the above calculations suggest. There is some level of robustness in the calculations, though.
Firstly, data from other stations for which short-term records are available, indicate that 2017’s rainfall in the Western Cape is indeed low, reaching 40-50 % of the mean of those short-term records. In 2017, CTA has recorded 35% of mean in the corresponding period. That proportion is clearly lower than elsewhere, but at least it is of a similar order of magnitude. Increasing the 2017 CTA rainfall by 50% would give a return interval of 80 years. This is still pretty rare.
Secondly, the multi-year calculations are more robust than the single-year ones. This is because while we might not be sure about this year’s data, we have confidence in the older data. The pre-2016 data I use are almost identical to the “official” SAWS record for CTA. And since the current year contributes only a fraction to the multi-year rainfall, eventual error in current year rainfall will have less influence on the final result. Again, if one considered that CTA rainfall in 2017 was actually 50% higher than what I have used in calculations, the return interval for the past 2,3 and 4-year rainfall total would be 490, 314 and 30 years.

Donovan
Thanks for an excellent analysis, really useful. I would take issue with exonerating the City of CT though – not because of the shortage, but because this drought did not happen overnight and demand management and enforemcement of restrictions has been catastrophically ineffective when it has long been obvious that remaining reserves are far below what is required to get through summer, even if normal patterns are restored.